Πώς να υπολογίσετε διάφορες παραμέτρους σωλήνων: βασικοί τύποι και παραδείγματα υπολογισμού

Νερό, θέρμανση, αποχέτευση, καμινάδα, περίβλημα, χαλκός, χάλυβας, πλαστικό, μεταλλικό πλαστικό, στενοί, φαρδιοί σωλήνες για διάφορους σκοπούς από διάφορα υλικά μας περιβάλλουν παντού. Η ανάγκη δημιουργίας νέων επικοινωνιών ή αντικατάστασης παλαιών προκύπτει τόσο κατά την κατασκευή του σπιτιού όσο και κατά την τρέχουσα επισκευή. Κατά την προετοιμασία ενός έργου για την επερχόμενη εργασία, δεν θα βλάψει να οπλιστείτε με μια αριθμομηχανή για να υπολογίσετε το βάρος του σωλήνα, τη μάζα, τον όγκο και άλλες παραμέτρους.

Γιατί πρέπει να υπολογίσετε τις παραμέτρους σωλήνων;

Ένας προκαταρκτικός υπολογισμός των παραμέτρων των σωλήνων είναι απαραίτητος σε πολλές περιπτώσεις. Για παράδειγμα, για σωστή επικοινωνία του αγωγού με άλλα στοιχεία του συστήματος. Οι σχεδιαστές και οι εγκαταστάτες όταν εργάζονται με σωλήνες χρησιμοποιούν δείκτες όπως:

• ακεραιότητα του αγωγού ·
• απώλεια θερμότητας;
• ποσότητα μόνωσης
• ποσότητα υλικού για προστασία από τη διάβρωση ·
• τραχύτητα της εσωτερικής επιφάνειας του σωλήνα κ.λπ.

Ως αποτέλεσμα, μπορείτε να προσδιορίσετε τον ακριβή αριθμό σωλήνων που απαιτούνται για ένα συγκεκριμένο σύστημα, καθώς και τα βέλτιστα χαρακτηριστικά τους. Οι σωστοί υπολογισμοί σας εξοικονομούν από το υπερβολικό κόστος για την αγορά και τη μεταφορά υλικού, επιτρέπουν στις ουσίες που βρίσκονται σε εξέλιξη να κινούνται με δεδομένη ταχύτητα για την πιο αποτελεσματική χρήση του συστήματος.

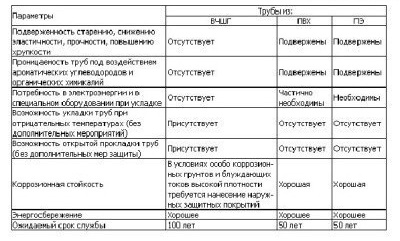
Αυτός ο πίνακας παρέχει μερικές χρήσιμες πληροφορίες σχετικά με τα χαρακτηριστικά διαφόρων τύπων σωλήνων, οι οποίοι θα σας βοηθήσουν να επιλέξετε τις σωστές δομές που απαιτούνται για τη δημιουργία του αγωγού.

Στα συστήματα θέρμανσης, η διάμετρος των σωλήνων εξαρτάται ουσιαστικά από την επιτρεπόμενη ταχύτητα. Ένα παράδειγμα αυτού του είδους υπολογισμού παρουσιάζεται στο βίντεο:

Υπολογισμοί διαφόρων παραμέτρων σωλήνων

Για τον σωστό υπολογισμό των κύριων παραμέτρων των σωλήνων, πρέπει να προσδιοριστούν οι ακόλουθοι δείκτες:

• υλικό από το οποίο κατασκευάζεται ο σωλήνας ·
• τύπος τμήματος σωλήνων ·
• εσωτερική και εξωτερική διάμετρος
• Πάχος τοιχώματος;
• μήκος σωλήνων κ.λπ.

Μέρος των δεδομένων μπορεί να ληφθεί απλώς μετρώντας το σχεδιασμό. Πολλές χρήσιμες πληροφορίες περιέχονται σε έγγραφα πιστοποίησης, καθώς και σε διάφορα βιβλία αναφοράς και τυπικές προδιαγραφές κατάστασης.

Πώς να γνωρίζετε τη διάμετρο και τον όγκο του σωλήνα;

Ορισμένοι τύποι υπολογισμού είναι εξοικειωμένοι με κάθε μαθητή. Για παράδειγμα, εάν πρέπει να αποσαφηνίσετε τη διάμετρο ενός συγκεκριμένου σωλήνα, θα πρέπει να μετρήσετε την περιφέρεια του. Για να το κάνετε αυτό, μπορείτε να χρησιμοποιήσετε μια ταινία εκατοστών, η οποία χρησιμοποιείται από μοδίστρες. Ή θα πρέπει να τυλίξετε τον σωλήνα με άλλη κατάλληλη ταινία και, στη συνέχεια, να μετρήσετε το προκύπτον τμήμα με ένα χάρακα.

Στη συνέχεια, χρησιμοποιούμε τον τύπο για την περιφέρεια:

L = πD, όπου:

• L είναι η περιφέρεια του κύκλου.
• π είναι ένας σταθερός αριθμός "pi" ίσος με περίπου 3,14.
• D είναι η διάμετρος του κύκλου.

Αρκεί να κάνετε έναν απλό μετασχηματισμό για να υπολογίσετε την εξωτερική διάμετρο του σωλήνα χρησιμοποιώντας αυτόν τον τύπο:

D = L / π.

Με τη μέτρηση του πάχους τοιχώματος του σωλήνα, είναι επίσης εύκολο να υπολογιστεί η εσωτερική διάμετρος του κύκλου. Για να γίνει αυτό, διπλασιάστε την τιμή του πάχους του τοιχώματος του σωλήνα από την τιμή της εξωτερικής διαμέτρου του σωλήνα.

Υπολογισμός της διατομής του σωλήνα

Για να υπολογίσετε τη διατομή του σωλήνα, υπολογίστε την περιοχή του κύκλου. Αυτό λαμβάνει υπόψη τη διαφορά μεταξύ της εξωτερικής διαμέτρου του σωλήνα και του πάχους των τοιχωμάτων του, με άλλα λόγια, της εσωτερικής διαμέτρου του σωλήνα.

Αυτό το σχήμα δείχνει σαφώς δείκτες όπως η εξωτερική διάμετρος του σωλήνα και το πάχος του τοιχώματος του. Η διαφορά μεταξύ της εξωτερικής διαμέτρου και του πάχους σας επιτρέπει να υπολογίσετε την εσωτερική διάμετρο του σωλήνα

Ο τύπος περιοχής κύκλου μοιάζει με αυτό:

S = πR², όπου:

• S είναι η περιοχή του κύκλου.
• π είναι ο αριθμός του "pi";
• Το R είναι η ακτίνα του κύκλου, υπολογιζόμενη ως η μισή διάμετρος.

Εάν χρησιμοποιείτε πληροφορίες σχετικά με την εξωτερική διάμετρο και το πάχος του τοιχώματος του σωλήνα, ο τύπος μπορεί να έχει την εξής μορφή:

S = π (D / 2-T) ², όπου:

• Το S είναι η περιοχή διατομής.
• π είναι ο αριθμός του "pi";
• D είναι η εξωτερική διάμετρος του σωλήνα.
• T είναι το πάχος του τοιχώματος του σωλήνα.

Ας υποθέσουμε ότι υπάρχει ένας σωλήνας του οποίου η εξωτερική διάμετρος είναι 1 μέτρο και το πάχος του τοιχώματος είναι 10 mm. Πρώτα πρέπει να συμφωνήσετε σε όλες τις ενότητες. Το πάχος του τοιχώματος θα είναι 0,01 μέτρα. Σύμφωνα με τον παραπάνω τύπο, υπολογίζουμε τη διατομή ενός τέτοιου σωλήνα:

S = 3,14Χ (1m / 2-0,01m) ² = 0,75m²

Έτσι, η διατομή του σωλήνα με τις καθορισμένες παραμέτρους θα είναι ίση με 0,75 τετραγωνικά μέτρα. Μ

Όπως γνωρίζετε, η ακρίβεια των υπολογισμών με τον αριθμό "pi" εξαρτάται από τον αριθμό των δεκαδικών ψηφίων που χρησιμοποιούνται κατά την εφαρμογή αυτής της σταθεράς. Ωστόσο, η κατασκευή συνήθως δεν απαιτεί εξαιρετικά ακριβείς υπολογισμούς και ο αριθμός pi θεωρείται ότι είναι 3,14. Το τελικό αποτέλεσμα έχει επίσης νόημα να στρογγυλοποιούνται με δύο δεκαδικά ψηφία.

Πώς να υπολογίσετε τον όγκο του σωλήνα;

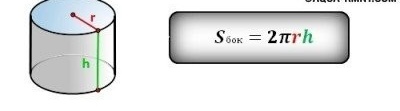
Αυτό το διάγραμμα απεικονίζει τη χρήση δεδομένων όπως η ακτίνα του τμήματος σωλήνα και το μήκος του για τον προσδιορισμό του όγκου του σωλήνα

Ο υπολογισμός του όγκου ενός συγκεκριμένου τμήματος σωλήνων δεν είναι επίσης δύσκολος. Για να το κάνετε αυτό, πρέπει πρώτα να βρείτε την περιφέρεια του σωλήνα από την εξωτερική του διάμετρο σύμφωνα με τον παραπάνω τύπο:

S = π (D / 2) ² ή S = πR²

Στην περίπτωση αυτή, το D είναι η εξωτερική διάμετρος του σωλήνα, και το R είναι η εξωτερική ακτίνα, δηλαδή η μισή διάμετρος. Μετά από αυτό, η ληφθείσα τιμή πρέπει να πολλαπλασιαστεί με το μήκος του τμήματος σωλήνα, έχοντας λάβει τον όγκο, ο οποίος εκφράζεται σε κυβικά μέτρα. Ο τύπος για τον υπολογισμό του όγκου του σωλήνα μπορεί να έχει την εξής μορφή:

V = SH, πού

• V είναι ο όγκος του σωλήνα, κυβικός Μ
• S - εξωτερική επιφάνεια διατομής, τ.μ.
• H είναι το μήκος του τμήματος σωλήνων, m

Ας υποθέσουμε ότι υπάρχει ένας σωλήνας με εξωτερική διάμετρο 50 cm και μήκος 2 μέτρα. Όλες οι μονάδες πρέπει να συμφωνηθούν πρώτα. D = 50 cm = 0,5 μ. Αντικαταστήστε αυτήν την τιμή στον τύπο της περιοχής κύκλου:

S = π (D / 2) ² = 3,14 (0,5 / 2) ² = 0,0625 m²

Τώρα μπορείτε να υπολογίσετε τον όγκο:

V = SH = 0,0625X2 = 0,125 m³.

Όλοι αυτοί οι υπολογισμοί μπορούν να γίνουν εύκολα χρησιμοποιώντας μια συμβατική αριθμομηχανή, αλλά είναι πολύ πιο βολικό να χρησιμοποιείτε τον κατάλληλο υπολογιστή που εκτελεί τον υπολογισμό στο διαδίκτυο.

Η αριθμομηχανή εκτελεί υπολογισμούς ανάλογα με τα αρχικά δεδομένα: σελακτίνα και ύψος βάσης, διάμετρος και ύψος βάσης ή επιφάνεια και ύψος βάσης.

Πώς να υπολογίσετε το βάρος του σωλήνα;

Οι πληροφορίες σχετικά με το βάρος ενός συγκεκριμένου αριθμού σωλήνων είναι απαραίτητες για την πρόβλεψη του κόστους μεταφοράς τους. Εάν χρησιμοποιείται μια μεγάλη δομή, το βάρος της δεν βλάπτει να συσχετιστεί με τη φέρουσα ικανότητα της βάσης της γνώσης.

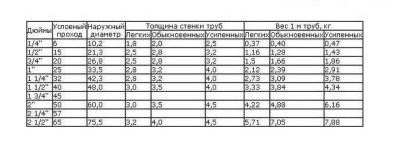
Αυτός ο πίνακας δείχνει δεδομένα αναφοράς για το βάρος των χαλύβδινων σωλήνων διαφόρων τύπων, λαμβάνοντας υπόψη τα μεγέθη και τα χαρακτηριστικά τους της τεχνολογίας παραγωγής

Οι μαθητές του Γυμνασίου γνωρίζουν καλά ότι η μάζα ενός αντικειμένου μπορεί να βρεθεί πολλαπλασιάζοντας τον όγκο του με την πυκνότητα της ουσίας από την οποία αποτελείται αυτό το αντικείμενο. Οι κατασκευαστές απαλλάσσονται από τους κουραστικούς υπολογισμούς της μάζας ενός συγκεκριμένου τμήματος σωλήνων, καθώς διάφοροι κατάλογοι κατασκευής περιέχουν πληροφορίες σχετικά με το βάρος ενός μετρητή λειτουργίας των διαφόρων τύπων σωλήνων.Ο ευκολότερος τρόπος είναι να υπολογίσετε τη μάζα του σωλήνα χρησιμοποιώντας τα σχετικά GOST, χρησιμοποιώντας πληροφορίες σχετικά με:

• το υλικό από το οποίο κατασκευάζεται ο σωλήνας ·
• η εξωτερική διάμετρος του
• πάχος τοιχώματος;
• εσωτερική διάμετρος κ.λπ.

Αφού ανακαλύψατε το βάρος ενός μετρητή λειτουργίας του σωλήνα, πολλαπλασιάστε την ληφθείσα τιμή με τον συνολικό αριθμό μετρητών λειτουργίας. Η πολυπλοκότητα της εργασίας αντιστοιχεί στο επίπεδο της τέταρτης έως πέμπτης τάξης ενός περιεκτικού σχολείου.

Για να μάθετε το βάρος των σωλήνων, σας προτείνουμε να χρησιμοποιήσετε την ηλεκτρονική μας αριθμομηχανή. Εισαγάγετε τις απαραίτητες πληροφορίες στα κατάλληλα πεδία, μετά τα οποία το πρόγραμμα εμφανίζει την τιμή βάρους του καθορισμένου αριθμού σωλήνων.